拓扑空间
拓扑空间
拓扑空间的定义
定义:[拓扑空间]
设$X$是一个非空集合,$X$的一个子集族$\tau$被称为是$X$的一个拓扑,当它满足以下三条公理:
- $X$和$\emptyset$在$\tau$中;
- $\tau$中任意多个成员的并集在$\tau$中;
- $\tau$中有限个成员的交集在$\tau$中.(由数学归纳法可得,等价于两个成员的交集在$\tau$中.)
集合$X$和它上边的一个拓扑被称为是拓扑空间记为$(X,\tau)$.$\tau$中的成员被称为是开集.当我们给出了集合$X$上的一个拓扑就是规定了什么样的子集是开集.
下边我们给出几个常用的拓扑的例子:
- (离散拓扑)设$X$是一个集合,$2^X$构成$X$上的 一个拓扑;显然任何一个子集都是$X$的开集;
- (平庸拓扑)设$X$是一个集,$\tau=\{X,\emptyset\}$构成了$X$的一个拓扑;这是最简单的拓扑;
- (余有限拓扑) 设$X$是无穷集合(有的书上没有这个要求,那样的余有限拓扑就没有太大意义),$\tau_f=\{A^c|A\text{是X的有限子集}\}\cup \{\emptyset\}$是$X$上的一个拓扑.(这里的$\tau_f$是因为有限的英文是finite)
- (余可数拓扑)设$X$是不可数集合(有的书上没有这个要求,那样的余可数拓扑就没有太大意义),$\tau_c=\{A^c|A\text{是X的可数子集}\}\cup \{\emptyset\}$是$X$上的一个拓扑.(这里的$\tau_c$是因为可数的英文是countable)
- (欧式拓扑)取$X=\mathbb{R}$,$\tau_{e}=\{U|U\text{是若干个开区间的并}\}$是$\mathbb{R}$上的一个拓扑.
这些例子都十分容易验证,为了熟悉拓扑空间的定义,我们选取其中一个稍显复杂的拓扑空间进行验证,比如4:
显然$\emptyset\in \tau$,而$X^c=\emptyset$故$X\in \tau$;
另外取$A_1,A_2$,$(A_1\cap A_2)^c=A_1^c\cup A_2^c$,两个可数集的并集是可数集,因此公理的第三条满足;
取$A_{\lambda},\lambda\in \Lambda$,那么:
可数集的交集当然是可数集,因此公理的第2条满足.
对于一个集合$X$而言,任给出一个拓扑,显然
因此离散拓扑是最大的拓扑,平庸拓扑是最小的拓扑;这里我们给出了似乎描述了拓扑的大小,为了精确化评判,我们必须下个严格的定义:
定义:拓扑的大小
设$\tau_1,\tau_2$是$X$上的两个拓扑,如果$\tau_1\subset \tau_2$,我们称$\tau_2$比$\tau_1$大,或者$\tau_2$比$\tau_2$细(可能有的书上给出的是相反的,理解即可.).
但是注意到,在包含的关系下,同一个集合$X$上定义的拓扑只是一个偏序关系而非是全序,因为不是所有的拓扑都可以比较大小(我们马上会给出实例)
首先我们可以看出$\tau_f$和$\tau_c$是可以比较的,$\tau_f\subset \tau_c$;
但是$\tau_e$和$\tau_c$不可比较:例如在$\mathbb{R}$中:因为$\tau_e$中元素的补集一般是不可数集所以不在$\tau_c$中,反之$\tau_c$中的元素一般也不能写为若干和开集的并,比如全体无理数.
度量拓扑
由于大家都已经学过度量空间,因此这里不再重述其定义:设$(X,d)$是一个度量空间,$d$是$X$上第一个度量函数,我们知道该度量函数可以定义出球形邻域:
类似欧式空间一样,用这些球我们也可以定义出$X$上的一个拓扑;但是注意到:所有的球组成的集合不能构成集合$X$的一个拓扑,很显然:比如两个球的并和交一般不是球!,但是类似欧式空间中,$X$上的拓扑可以定义为:
下边我们证明$\tau_d$确实是$X$上的一个拓扑:
显然第一条公理是自然满足的;第二条公理也是满足的。下边我们主要证明第三条:两个$\tau_d$中的元素的交集还在$\tau_d$中.为此我们需要引理:两个球的交集是若干个球的并集:
引理 $(X, d)$ 的任意 两个球形邻域的交集是若 干球形邻域的并集,
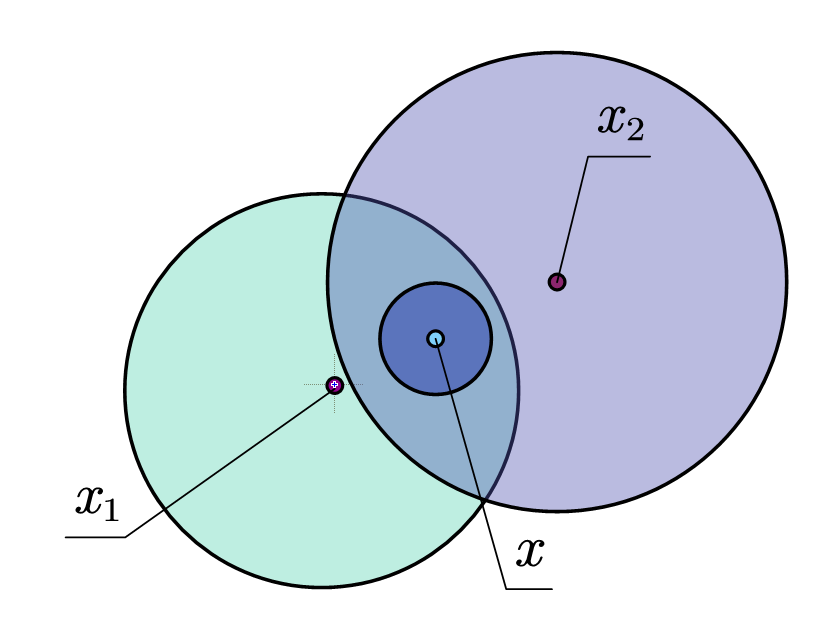
这个定理的证明,我们可以说是相当熟悉了!设 $U=B\left(x_{1}, \varepsilon_{1}\right)$ $\cap B\left(x_{2}, \varepsilon_{2}\right), \quad \forall x \in U$, 则 $\varepsilon_{1}-d\left(x, x_{1}\right)>0(i=1,2) .$ 记 $\varepsilon_{x}=\min \left\{\varepsilon_{1}-d\left(x, x_{1}\right)\right.$, $\left.\varepsilon_{2}-d\left(x, x_{2}\right)\right\}$ , 不难验证 $B\left(x, \varepsilon_{x}\right) \subset U$. 于是
下边我们就开始证明两个$\tau_d$中的元素$U_1,U_2$在$\tau_d$中:
那么:
又因为我们的引理可知:
所以$U_1\cap U_2\in \tau_d$中,因此任何一个度量都可以诱导出一个$\tau_d$!
一个拓扑如果可以被度量诱导出来的空间称为是可度量的,一个可度量的拓扑空间装备了相应的度量就成为了度量空间,我们知道度量空间是由很多好的性质,比如说序列收敛的唯一性(满足Hausdorff公理).因此我们会对什么时候一个拓扑能够被度量化十分感兴趣,一个很自然的问题就是:是否所有的拓扑都可以被度量化?很遗憾我们的回答是不可以,我们下边会举出一个不可被度量化的例子;既然不是所有的都可被度量,那么自然探究的就是什么条件可以被度量,深入的问题我们不想在这里讨论,在后边的章节我们会就具体的问题讨论!下边只是对以上所述做一些简单的讨论:
例:不妨考虑$\{a,b,c\}$,拓扑定义为平庸拓扑,所以$X$中的开集只有$\emptyset,X$,但是如果存在度量$d$,那么$d(a,a)=0,d(a,b),d(a,c)\ne 0$我们记较小者记为$r$,所以$B(a,r)$是一个球形邻域,但是$B(a,r)=\{a\}\notin \tau$,因此这个拓扑不可以被度量化.
这里我们只是简单对其做了说明,具体关于可度量化的讨论,我们会在后续中详细讨论.
拓扑基
在度量空间我们在定义由拓扑的时候我们可以看到本身这些球是不可以定义出一个拓扑的,但是利用若干个球的并就可以定义出度量拓扑。对于我们而言当然是希望用更简单的东西来描述一个事物,既然能用这些球形邻域说清楚,我们就可以不非要用$\tau_d$来说,类似的我们在其他拓扑也有类似的定义:
设 $\mathscr{B}$ 是 $X$ 的一个子集族, 规定新子集族:
称$\overline{\mathscr{B}}$是由$\mathscr{B}$生成的子集族.显然$\mathscr{B}\subset \overline{\mathscr{B}}$,且$\emptyset\in \overline{\mathscr{B}}$.
从度量空间中由度量函数诱导出的度量拓扑,我们可以发现:利用球形邻域能够定义出度量拓扑是因为它满足
球形邻域的并可以包含整个空间;
$\tau_d=\{U|U\textbf{是若干个球的并集;可以是不可数个/可数个/有限个/0个}\}$满足三条拓扑公理.
由度量拓扑定义,我们很自然的给出拓扑基的定义:
定义:拓扑基
称集合 $X$ 的子集族 $\mathscr{B}$ 为集合 $X$ 的拓扑基, 如果 $\overline{\mathscr{B}}$ 是 $X$ 的一个拓扑.
以及判断拓扑基的方法:
[命题]:$\mathscr{B}$ 是集合 $X$ 的拓扑基的充分必要条件是:
$\bigcup\limits_{B \in \mathscr{B}} B=X$;
若 $B_{1}, B_{2} \in \mathscr{B}$, 则 $B_{1} \cap B_{2} \in \overline{\mathscr{B}}$ (也就是 $\forall x \in B_{1} \cap B_{2}$, 存在 $B \in \mathscr{B}$ , 使得 $x \in B \subset B_{1} \cap B_{2}$ ).
必要性的证明是显然的:因为$\overline{\mathscr{B}}$是$X$的一个拓扑,因此$X\in \overline{\mathscr{B}}$,自然第一条就要满足;而$B_1,B_2\in \overline{\mathscr{B}}$所以他们的交集在$\overline{\mathscr{B}}$中.
下证充分性:即$\overline{\mathscr{B}}$满足三条公理:
$\emptyset$和$X$在其中以及并集公理是自然满足的;下边只用看交集公理是否满足:任取$\overline{\mathscr{B}}$中的两个元素$A_1,A_2$(为了和定理中的$B_1,B_2$区分.)
那么:
所以:
故定理得证.
上边所述是在集合$X$上没有拓扑时,我们用一个子族生成其拓扑;但是一个空间如果已经有了拓扑,我们希望尽可能用较少的元素描述其拓扑,这时就衍生除了拓扑空间的拓扑基!
定义:[拓扑基’]
称拓扑空间 $(X, \tau)$ 的子集族 $\mathscr{B}$ 为这个拓扑空间的拓扑基, 如果 $\overline{\mathscr{B}}=\tau$.
仔细思考不难得到其判定定理:
定理
$\mathscr{B}$ 是拓扑空间 $(X, \tau)$ 的拓扑基的充分必要条件为:(1) $\mathscr{B}\subset \tau$(即$\mathscr{B}$的成员是开集);
(2) $\tau \subset \overline{\mathscr{B}}$ (即每个开集都是 $\mathscr{B}$ 中一些成员的并集).
似乎比较显然.
子基
我们看到了,如果$\mathscr{B}$是$X$的一组基,那么就要对它有所要求,因此不是所有集族都可以生成拓扑,那么任意给出一个集族,是否可以找到一个最小的拓扑包含它呢?下边的定理给出了问题的回答:
[定理:]若 $\mathscr{S}$ 为任意非空的集族, 则 $\mathscr{S}$ 的元的所有有限交 的族是关于集 $X=\bigcup\{S:S\in\mathscr{S}\}$的某个拓扑的基
注意到:此时集合取为了$X=\bigcup\{S:S\in\mathscr{S}\}$
若 $\mathscr{S}$ 为一个集族, $\mathscr{B}$ 为 $\mathscr{S}$ 的元的所有有限交的族, 则 $\mathscr{B}$ 的两个元的交仍为 $\mathscr{B}$ 的元,再应用上一定理便知 $\mathscr{B}$ 是某个 拓扑的基. (至于这个基是什么,通过上个题的证明,我想大家是可以看出来的!)
有了上边的定理,我们给出子基的定义:
定义:[子基]我们称集族 $\mathscr{S}$ 为拓扑 $\mathscr{T}$ 的子基当且仅当 $\mathscr{S}$ 的元的所有有 限交的族为 $\mathscr{T}$ 的基 (即当且仅当 $\mathscr{T}$ 的每一个元是 $\mathscr{S}$ 的元的有 限交的并).
我们可以给出一个不太有趣的子基的例子:
最自然的子基是: 所有半无限开区间的族, 即所有形如 $\{x: x > a \}$ 或 $\{x: x<a\}$ 的集组成的族. 因为每一个开区间是两个如此 的集的交, 故该族是一个子基.
有了拓扑基之后,我们比较不同拓扑之间的大小就会更方便!下边就给出用拓扑基比较大小的判定定理:
[定理]:设 $\mathcal{B}$ 和 $\mathcal{B}^{\prime}$ 分别是 $X$ 的拓扑 $\mathcal{T}$ 和 $\mathcal{T}^{\prime}$ 的基. 则下列条件等价:
(1) $\mathcal{T}^{\prime}$ 细于 $\mathcal{T}$.
(2) 对于每一个 $x \in X$ 及包含 $x$ 的每一个基元素 $B \in \mathscr{B}$, 存在一个基元素 $B^{\prime} \in \mathscr{B}^{\prime}$, 使得 $x \in B^{\prime} \subset B$
证 $(2) \Rightarrow(1)$. 对于 $\mathcal{T}$ 的一个元素 $U$, 我们证明 $U \in \mathcal{T}^{\prime}$. 取 $x \in U$. 因为 $\mathcal{B}$ 生成 $\mathcal{T}$, 则存 在一个元素 $B \in \mathscr{B}$, 使得 $x \in B \subset U$. 条件 ( 2 ) 告诉我们, 存在一个元素 $B^{\prime} \in \mathscr{B}^{\prime}$, 使得 $x \in B^{\prime} \subset$ B. 于是 $x \in B^{\prime} \subset U$. 根据定义 $U \in \mathcal{T}^{\prime}$.
$(1) \Rightarrow(2)$. 给定 $x \in X$ 和 $B \in \mathscr{B}$, 其中 $x \in B$. 根据定义, $B \in \mathcal{T}$, 再根据条件 (1), $\mathcal{T} \subset$ $\mathcal{T}^{\prime}$. 因此 $B \in \mathcal{T}^{\prime}$. 因为 $\mathcal{B}^{\prime}$ 生成 $\mathcal{T}^{\prime}$, 所以存在一个元素 $B^{\prime} \in \mathscr{B}^{\prime}$, 使得 $x \in B^{\prime} \subset B$.
后边我们将频繁利用这个定理来比较一个集合上不同拓扑的大小!
设 $B$ 为实直线上所有开区间
的族. 由 $\mathscr{B}$ 生成的拓扑称为实直线上的标准拓䃼 (standard topology). 当我们考虑 $\mathbb{R}$ 时, 若无 特别声明, 我们将总假设考虑的是这个标准拓扑. 设 $\mathcal{B}^{\prime}$ 为所有半开区间
的族, 其中 $a < b$. 由 $\mathscr{B}^{\prime}$ 生成的拓扑称为 $\mathbb{R}$ 的下限拓扑 (lower limit topology). 具有下限拓扑的 $\mathbb{R}$ 记作 $\mathbb{R}_ {\ell}$. 对于 $n \in \mathbb{Z}+$, 令 $K$ 表示所有形如 $\frac{1}{n}$ 的数所组成的集合, 今 $\mathscr{B}^{\prime \prime}$ 是由所有开区间 $(a, b)$ 及形如 $(a, b)-K$ 形式的集合的族. 由 $\mathscr{B}^{\prime \prime}$ 所生成的拓扑称为 $\mathbb{R}$ 上的 $K$-拓扑( $K$ - topology). 具有 $K$-拓扑的 $\mathbb{R}$ 记作 $\mathbb{R}_{K}$.
现在我们就可以来比较这三个拓扑的大小了!
$\mathbb{R}_ {\ell}$ 和 $\mathbb{R}_{K}$ 的拓扑都严格细于标准拓扑, 但它们之间不可比较.
以 $\mathcal{T}, \mathcal{T}^{\prime}, \mathcal{T}^{\prime \prime}$ 分别表示 $\mathbb{R}, \mathbb{R}_{\ell}, \mathbb{R}_{K}$ 中的拓扑. 任意给定 $\mathcal{T}$ 中的一个基元素 $(a, b)$ 以 及一个点 $x \in(a, b), \mathcal{T}^{\prime}$ 中的元素 $[x, b)$
包含着 $x$ 并且包含于 $(a, b)$. 另一方面, 任意给定 $\mathcal{T}^{\prime}$ 中的一个基元素 $[x, d)$, 却不存在 $\mathcal{T}$ 中的元素 $(a, b)$, 使得它包含于 $[x, d)$ 同时又包含着 $x$. 因此 $\mathcal{T}^{\prime}$ 严格细于 $\mathcal{T}$.
对 $\mathbb{R}_{K}$ 进行类似的讨论. 任意给定 $\mathcal{T}$ 中的一个基元素 $(a, b)$ 以及一个点 $x \in(a, b)$, 则 $(a, b)$ 是 $\mathcal{T}^{\prime \prime}$ 中的一个基元素并且包含着 $x$. 另一方面, 任意给定 $\mathcal{T}^{\prime \prime}$ 中的一个基元素 $B=(-1,1)-K$ 以及 $B$ 中一个点 0 , 却不存在包含于 $B$ 中并且包含着 0 的开区间.
拓扑空间中的点集
鉴于这部分我们在欧式空间中已经学过了,因此我们不再重复各种证明:
[邻域、内点和内部]
设$A$是拓扑空间$(X,\tau)$的一个子集,点$x\in A$.如果存在开集$U$使得$x\in U\in A$,则称$x$是$A$的一个内点,$A$是$x$的一个邻域,$A$的所有内点的集合称为$A$的内部,记为$A^{\circ}$.
它具有以下性质:
- 若 $A \subset B$, 则 $A^{\circ} \subset B^{\circ}$;
- $A^{\circ}$ 是包含在 $A$ 中的所有开集的并集,因此是包含在 $A$ 中 的最大开集;该条可以作为内部的等价定义.
- $A^{\circ}=A\iff A$是开集;
- $(A \cap B)^{\circ}=A^{\circ}\cap B^{\circ}$;
- $(A \cup B)^{\circ} \supset A^{\circ}\cup B^{\circ}$.
我们不想对上述事实进行证明,感兴趣的读者可以自行尝试.
[闭集]:拓扑空间$(X,\tau)$的一个子集$A$成为闭集,如果$A^c$是开集.其满足以下三条公理(De Morgan法则):
- $X$和$\emptyset$是闭集;
- 任意多闭集的交集是闭集;
- 有限个闭集的并集是闭集.
以上的定义是依赖开集定义的闭集,事实上我们也可以利用闭集自己的性质独立定义闭集,这需要用的聚点的概念:
[聚点与闭包]:设 $A$ 是拓扑空间 $X$ 的子集, $x \in X .$ 如果 $x$ 的每个邻域都含有 $A \backslash\{x\}$ 中的点,则称 $x$ 为 $A$ 的聚点. $A$ 的所有聚点的 集合称为 $A$ 的导集, 记作 $A^{\prime}$. 称集合 $\bar{A}:=A \cup A^{\prime}$ 为 $A$ 的闭包.
由定义不难推出 : $x \in \bar{A} \longleftrightarrow x$ 的任一邻域与 $A$ 都有交点.
唯一一个本节证明的命题:
定理:若拓扑空间$X$的自己$A$和$B$互为余集,则$\bar{A}$和$B^{\circ}$互为余集.
同样的,根据对偶率,闭集也有同样的性质:
- 若 $A \subset B$, 则 $\bar{A} \subset \bar{B}$;
- $\bar{A}$ 是所有包含 $A$ 的闭集的交集,所促是含 $A$ 的最小的 闭集;该条可以直接作为闭集的等价定义
- $\bar{A}=A \Longleftrightarrow A$ 是闭集;
- $\overline{A \cup B}=\bar{A} \cup \bar{B}$;
- $\overline{A \cap B} \subset \bar{A} \cap \bar{B}$.
以上证明方式都和我们在数学分析或者实分析中的证明方式几乎雷同,唯一注意的就是,大家必须要对开集和闭集有全新的认识,我们下边举一个例子可以验证读者对开集和闭集的理解:
练习:取$X$为$\mathbb{R}^2$(以后我们更习惯记为$\mathbb{E}^2$)中$x\ge 1,x\le -1$的所有点构成的集合,拓扑为$\mathbb{E}^2$的拓扑,记$A$为$X$中第一个坐标大于0的集合,问集合$A$在$X$中是否是闭集?是否是开集.
如果你的答案:$A$是开集且是闭集那么说明你对开集和闭集有了基本的理解.
现在我们来总结以下关于闭包的性质:
1.$\bar{\varnothing}=\varnothing$;
2.$A \subset \bar{A};$
3.$\overline{A \cup B}=\bar{A}\cup \bar{B};$
4.$\bar{A}=\bar{\bar{A}}$.
事实上,这四条性质可以完全描述闭包:
闭包公理:设 $X$ 是一个集合. 映射 $c^{*}: \mathscr{P}(X) \rightarrow \mathscr{P}(X)$ 如 果满足条件:对于任何 $A, B \in \mathscr{P}(X)$,
(1) $c^{\ast}(\varnothing)=\varnothing$;
(2) $A \subset c^{\ast}(A)$;
(3) $c^{\ast}(A \cup B)=c^{\ast}(A) \cup c^{\ast}(B) ;$
(4) $c^{\ast}\left(c^{\ast}(A)\right)=c^{\ast}(A)$,
则称为集合 $X$ 的一个闭包运算. (以上四个条件通常称为 Kuratovski 闭包公理. )下边为了叙述方便,我们将$c^$运算记为$A^$,记$c^(A)=A^$.
则存在 $X$ 的惟一一个拓扑 $\mathscr{T}$ 使得在拓扑空间 $(X, \mathscr{T})$ 中对于每一个 $A \subset X$ 有 $c^{\ast}(A)=\bar{A}$.
我们先思考对应的拓扑应该是什么:如果$A^$是闭包,那么意味着它是闭集,那么满足$A^=A$的就是闭集,所以他们的补集应该是开集;所以我们猜想对应的拓扑就是:
下边我们验证它确实是一个拓扑:
1.首先由于$\varnothing^{\ast}=\varnothing$ 所以 $\varnothing^c=X\in \mathscr{T}$,其次由于公理的第二条:显然$X\subset X^{\ast}\subset X$,所以$X^{\ast}=X$,意味着$X^c=\varnothing\mathscr{T}$,所以拓扑公理的第一条自然满足;
2.任取$A_1\cdots,A_n\in \mathscr{T}$,我们看他们的交集的补集是否满足公理:
因此拓扑公理中的闭集公理满足;
3.最难的是并集公理,我们任取$A_{\lambda}\in\mathscr{T} ,\lambda\in \Lambda$,应该验证:
满足闭包公理.
首先我们要说明,如果$A\subset B$那么$A^{\ast}\subset B^{\ast}$,因为$B=A\cup (B-A)$,再利用闭包公理的第3条即可.
首先:
闭包公理的第二条;现在证明反向.
因为任意的$\lambda\in \Lambda$都有:
所以:
根据闭包公理的第四条可以得到:
因此:
故另一边也得到了证明,所以这是一个拓扑.
下边我们说明$A^{\ast}$是$A$的闭包.因为$A^{\ast}=A^{\ast\ast}$所以$A^*$是一个闭集,因此$\bar{A}\subset A^{\ast}$,其次又因为:
所以:
又因为$\bar{A}$是闭集,所以$\bar{A}^*=\bar{A}$,故
故命题得证.
最后我们证明唯一性:
假设还有一个拓扑也是由闭包公理确定的,那么我们知道$A^*$是闭包,一个子集是闭集当且仅当它的补集是开集,所以两个拓扑的开集都相同,自然是相同的拓扑.
序列的收敛
最后在本节中我们引入序列收敛的定义.这里我们仍然还是用大家最为熟知的序列$\{x_n\}$的形式,事实上点集的收敛并不是一个什么简单的事情,我们会在补充内容中引入网、滤子等概念来完善点集收敛.这里我们先给出形如数学分析中点列收敛的定义:
[序列收敛]设$\{x_n\}$是拓扑空间$X$中的点列,如果$x_0\in X$的任一邻域$U$都包含$\{x_n\}$的几乎所有项(即只有有限项在邻域$U$外或存在正整数$N>0$,任意$n>N$,$x_n$在邻域$U$中),则称$x_n$收敛到$x_0$,记为$x_0\to x_0$.
但是这种序列的收敛失去了我们在数学分析中序列收敛的良好性质,比如::序列收敛的极限是不唯一的!(这是一个很基本的反例!)
考虑$(R,\tau_f)$只要序列$\{x_n\}$中两两不同,则任一点$x\in R$的邻域都包含$\{x_n\}$的几乎所有项,从而$x_n\to x$
对于$(R,\tau_e)$,我们也可以举出类似的反例.比如$\{\frac{1}{n}\}$可以收敛到实直线上的任何一点.
子空间
设$A$是拓扑空间$(X,\tau)$的一个非空子集
[子空间]
规定 $A$ 的子集族容易验证 $\tau_{A}$ 是 $A$ 上的一个拓扑,称为 $\tau$ 导出的 $A$ 上的子空间拓扑,称 $\left(A, \tau_{A}\right)$ 为 $(X, \tau)$ 的子空间.
如果不做说明,当我们谈及拓扑空间的子集总是将其看作子空间.
那么这样自然就会产生一个问题,如果$B\subset A\subset X$,那么将$B$看作是$A$的子空间时会产生一个拓扑,看作$X$的子空间时会产生一个拓扑,这两个拓扑是否相同呢?答案是肯定的:
事实上它们是一样的,记 $\left(\tau_{A}\right)_{B}$ 是 $\tau_{A}$ 导出的 $B$ 上的拓 扑,则
我们已经看到了$A$是$X$的一个子空间,如果$B$是$X$上的一个开集,当且仅当它是$X$中的一个开集与$A$的交集,那么对于闭集是否有类似的结论,即:$B$为$A$上的闭集是否等价于是$X$中的一个闭集与$A$的交集.
定理
设$X$是拓扑空间,$C\subset A\subset X$则$C$是$A$的闭集$\iff$$C$是$A$与$X$的一个闭集之交集.
$C$ 是 $A$ 的闭集 $\Longleftrightarrow A \backslash C$ 是 $A$ 的开集
$\Longleftrightarrow$ 存在 $X$ 中开集 $U$, 使得 $A \backslash C=U \cap A$
$\Longleftrightarrow$ 存在 $X$ 中开集 $U$,使得 $C=U^c \cap A$
$\Longleftrightarrow C$ 是 $X$ 中一个闭集与 $A$ 之交集.
应用子空间中开集和闭集的定义我们就可以得到如下定理:
定理
设 $X$ 是拓扑空间, $B \subset A \subset X$, 则
(1):若 $B$ 是 $X$ 的开(闭)集,则 $B$ 也是 $A$ 的开(闭)集;
(2):若 $A$ 是 $X$ 的开(闭)集, $B$ 是 $A$ 的开(闭)集,则 $B$ 也是 $X$ 的开 (闭) 集.
(1):如果$B$是$X$中的开集,那么$B=B\cap A$因此是$A$种的开集;闭集同理;
(2):如果$B$是$A$中的开集,那么:
又因为$A$也是开集,所以$B$是$X$中的开集.
注意到$A$是$X$中的开集或者闭集不可缺少.
连续映射
接下来进入拓扑学研究的重要课题之一:连续映射和同胚映射:
在数学分析中我们曾经定义过连续性,下边我们看看在数学分析中我们是怎样定义的:
设 $f: \boldsymbol{E}^{1} \rightarrow \boldsymbol{E}^{1}$ 是一个函数, $x_{0} \in \boldsymbol{E}^{1} . f$ 在 $x_{0}$ 处连续的含义有多种描述方法,例如:
用序列证言: 如果序列 $\left\{x_{n}\right\}$ 收敛到 $x_{0}$ ,则序列 $\left\{f\left(x_{n}\right)\right\}$ 收敛到 $f\left(x_{0}\right) ;$
用 $\varepsilon-\delta$ 叙述: 对任意正数 $\varepsilon>0$, 总可找到 $\delta>0$,使得当 $\left|x-x_{0}\right|$ $<\delta$ 时, $\left|f(x)-f\left(x_{0}\right)\right|<\varepsilon$;
用开集语言叙述:若$V$是包含$f(x_0)$的开集,则存在包含$x_0$的开集$U$,使得$f(U)\subset V$.
那么在一般的拓扑空间中,我们怎样才能把连续的概念给保留下来呢?
观察第一种说法,由于拓扑保留了最简单的性质,因此我们需要额外定义序列的收敛(当然,我们引入序列的收敛性也并非不可.我们后边会专门介绍序列的收敛.)
第二种可以直接被否定,因为它用到了度量的性质,而我们之前已经看到了并非所有拓扑都可以度量化;
第三种,则可以用来定义拓扑中的连续,因为它仅用到了开集这种最基本的事物,而一个最简单的拓扑中也只有这些东西,因此我们给出一般的拓扑空间中连续性的定义.
[连续映射]
设 $X$ 和 $Y$ 都是拓扑空间, $f: X \rightarrow Y$ 是一个映射, $x$ $\in X .$ 如果对于 $Y$ 中 $f(x)$ 的任一开集 $V, f^{-1}(V)$ 总是 $x$ 的开集,则 说 $f$ 在 $x$ 处连续.当映射$f$在$X$中的每一点都连续时,则称$f$是连续映射.(上述定义中的开集可以改为邻域或者开邻域.)
注意到:我们在定义时并不要求$V$是$f(X)$的子集,事实上,倘若存在$x\notin f(X)$,我们将其映回为$\emptyset$.
有了开集、闭集和拓扑基的定义之后我们可以证明下列几个说法是等价的:
定理
下列各条是等价的:(a) $f: X \rightarrow Y$ 是连续映射;
(b) 若 $\beta$ 是 $Y$ 的一组拓扑基, $\beta$ 内每个成员的原象为 $X$ 的开集,
(c) $f(\bar{A}) \subseteq \overline{f(A)}$, 对于 $X$ 的任何子集 $A$;
(d) $\overline{f^{-1}(B)} \subseteq f^{-1}(\bar{B})$, 对于 $Y$ 的任何子集 $B$;
(e) $Y$ 内任何闭集的原像为 $X$ 的闭集.
我们采用循环证明的方法:
$(a)\Rightarrow (b)$:由定义开集的原像任意是开集,而每个拓扑基成员是开集,因此显然成立;
$(b)\Rightarrow (c)$:显然我们有:$f(A)\subset \overline{f(A)}$,因此,我们只需要证明对任意的$x\in \bar{A}-\bar{A}$,如果$f(x)\notin f(A),$那么$f(x)$必然是$f(A)$的极限点.设$N$是$f(x)$在$Y$中的一个开集,则存在开集可以用拓扑基的并表示为$B$,那么$f(x)\in B\subset N$.假设$(b)$成立,那么$f^{-1}(B)$的原像是开集,从而是$x$的一个邻域,而$x$是$A$的极限点,因此$f^{-1}(B)$中必有$A$中的点,因此$B$从而$N$含有$f(A)$中的点,得到所证.(注意到极限点的定义.)
$(c)\Rightarrow(d)$:直接取$\bar{A}=\overline{f^{-1}(B)}$即得证.
$(d)\Rightarrow (e)$:若$B$是$B$集,那么从$(c)$中就可以看出:
得证.
$(e)\Rightarrow (a)$:对闭集取补即可.
注意到,我们在定义连续映射时说开集的原像是开集,此时的开集并没有一定要使开集落在$f(X)$中,因此可以放心的使用各种集合论中的 手段.
下边我们看一下连续映射有哪些性质:
$\boxed{\text{连续映射的性质}}$
定理:设 $f: X \rightarrow Y$ 是一映射, $A$ 是 $X$ 的子集, $x \in A$. 记 $f_{A}=f \mid A: A \rightarrow Y$ 是 $f$ 在 $A$ 上的限制,则
(1) 如果 $f$ 在 $x$ 连续,则 $f_{A}$ 在 $x$ 也连续;
(2) 若 $A$ 是 $x$ 的邻域, 则当 $f_{A}$ 在 $x$ 连续时, $f$ 在 $x$ 也连续.
(1)设 $V$ 是 $f_{A}(x)=f(x)$ 的邻域,则 $f^{-1}(V)$ 是 $x$ 在 $X$ 中的邻域, 即存在开集 $U$, 使得 $x \in U \subset f^{-1}(V)$. 而$f_{A}{ }^{-1}(V)=$ $A \cap f^{\prime}(V) \supset A \cap U$, 这里 $A \cap U$ 是 $A$ 的包含 $x$ 的开集. 这就验证 $了 f_{A}$ 在 $x$ 的连续性.
(2)设 $V$ 是 $f(x)$ 的邻域,根据条件存在 $A$ 中的开集 $U_{A}$, 使 得 $x \in U_{A} \subset f_{A}^{-1}(V)=A \cap f^{-1}(V)$. 设 $U_{A}=U \cap A$,其中 $U$ 是 $X$ 的 开集. 则 $U \cap A^{\circ}$ 也是 $X$ 的开集, 且 $x \in U \cap A^{\circ} \subset U_{A} \subset f^{1}(V)$. 因此 $f$ 在 $x$ 连续.
下边介绍几个经典的连续映射:
恒同映射:id : $X \rightarrow X$ (即 id $(x)=x, \forall x \in X$ ) 是连续映射.(\hs{注意到:这里的两个$X$是指完全相同的拓扑空间,而非仅仅是集合的相等,读者可以举出例子,如果两边装备的拓扑不同,即使是恒同映射也难以做到连续映射!})
含入映射:设 $A$ 是 $X$ 的子空间, 记 $i: A \rightarrow X$ 是包含映射 (即 $i(a)=a$, $\forall a \in A)$, 则 $i$ 是连续映射, 因为当 $U$ 是 $X$ 的开集时, $i^{-1}(U)=$ $A \cap U$ 是 $A$ 的开集.
常值映射:如果 $f: X \rightarrow Y$ 是常值映射,即 $f(X)$ 是 $Y$ 中一点 $y_{0}$, 则 $f$ 连 续,因为 $f^{-1}(V)=X\left(\right.$ 若 $\left.y_{0} \in V\right)$, 或 $f^{-1}(V)=\varnothing$ (若 $y_0\notin V)$.
离散拓扑/平庸拓扑:如果 $X$ 是离散拓扑空间,或 $Y$ 是平凡拓扑空间, 则 $f: X \rightarrow Y$ 一定是连续的.(请证明!)
下边一个例子可以说明:虽然两个集合作为集合本身是相等的,但是如果两边的拓扑不同,即使是恒同映射,那么映射也不是连续的!
反例:设 $\mathbb{R}$ 为具有通常拓扑的实数集. $\mathbb{R}_{\ell}$ 为具有下限拓扑的实数集. 令
为恒等函数, 即对于每一个实数 $x, f(x)=x .$ 但是 $f$ 不是一个连续函数. 因为 $\mathbb{R}_{\ell}$ 的开集 $[a, b)$的原像还是 $[a, b)$, 它不是 $\mathbb{R}$ 的开集. 而另一方面, 恒等函数
[复合映射]
设 $X, Y$ 和 $Z$ 都是拓扑空间,映射 $f: X \rightarrow Y$ 在 $x$ 处连续, $g: Y \rightarrow Z$ 在 $f(x)$ 处连续;则复合映射 $g \circ f: X \rightarrow Z$ 在 $x$ 连续.
该定理我们已经证明了很多遍,请大家自行尝试!
下边的一个定理,是非常重要的一个定理,它是我们构造连续映射或者同胚映射常用的手段,被称为焊接引理或者粘贴引理,我们在这里给出较为简单的形式,后边会看到更加一般的形式;在此之前,让我们先引入几个基本概念:
设 $\mathscr{T} \subset 2^{X}$ 是拓扑空间 $X$ 的子集族,称 $\mathscr{B}$ 是 $X$ 的一个覆盖,如果 $\bigcup_{C \in \mathscr{T}} C=X$ (即 $\forall x \in X$至少包含在$\mathscr{T}$ 的一个成员中).如果覆盖的每个成员都是开(闭)集,则我们称对应的覆盖为开(闭)覆盖; 如果覆盖只包含有限个成员时,称 $\mathscr{C}$ 是有限覆盖.
[粘贴引理]
设 $\left\{A_{1}, A_{2}, \cdots, A_{n}\right\}$ 是 $X$ 的一个有限闭 覆盖. 如果映射 $f: X \rightarrow Y$ 在每个 $A_{i}$ 上的限制都是连续的,则 $f$ 是 连续映射.
只需要证明闭集的原像是闭集即可.
设 $B$ 是 $Y$ 的闭 集,记 $f_{A_{r}}$ 是 $f$ 在 $A_{z}$ 上的限制,则
$\forall i, f_{A_i}$ 是连续的,因此 $f_{A_{i}}^{-1}(B)$ 是 $A_{i}$ 的闭集. 又因为 $A$, 是 $X$ 的闭 集, 所以 $f_{A_{1}}^{-1}(B)$ 也是 $X$ 的闭集 $f^{-1}(B)$ 作为有限个闭集的并集也是闭集.
现在我们再次回头来说明一般拓扑空间中序列收敛丧失的良好性质!在数学分析中:我们曾用序列定义函数的连续性!对任意的$\varepsilon>0$,如果对任何的$x_n\to x_0$,都有$f(x_n)\to f(x_0)$则称函数$f(x)$在$x_0$点连续;但是在一般的拓扑空间中,我们却没有这样的性质!如果函数$f:X\to Y$是连续的,那么只能正面推,但是反之不行,这里举出一个反例!
例如:取$X$为不可数集合,拓扑为余可数拓扑,$Y$是离散的拓扑空间,那么$x_n\to x$时,对$n$充分大的时候$x_n=x$,从而$f(x_n)\to f(x)$.但是我们只要令$f$为某个单射,他就不可能是连续的.这是因为$\{f(x)\}$是$f(x)$的邻域,但其原像是$\{x\}$不是开集!(正面推可以留作习题训练!)
同胚映射
下边将进入拓扑学研究核心内容之一:同胚映射及同胚映射下的不变量:
[同胚映射]
如果 $f: X \rightarrow Y$ 是 一一对应, 并且 $f$ 及其逆 $f^{-1}$; $Y \rightarrow X$ 都是连续的,则称 $f$ 是一个同胚映射,或称拓扑变换,或简称同胚. 当存在 $X$ 到 $Y$ 的同胚映射时, 就称 $X$ 与 $Y$ 同胚,记作 $X$ $\cong Y$
必须强调的一点是:$f$和$f^{-1}$都连续的条件是不可缺少的!
$f^{-1}$ 连续这个条件是说, 对于 $X$ 的每一个开集 $U$, 在 $f^{-1}: Y \rightarrow X$ 下它的原像是 $Y$ 中的开 集. 但是, $U$ 在映射 $f^{-1}$ 下的原像就是 $U$ 在映射 $f$ 下的像. 于是, 可以用另一种 方式将问胚定义为一一映射 $f: X \rightarrow Y$, 使得 $f(U)$ 是一个开集的充分必要条件是 $U$ 是一个 开集.
下边我们就给出一个例子说明为何定义同胚时只给出$f$一一映射且连续时推不出$f^{-1}$也是连续的!
反例:
设 $S^{1}$ 表示单位圆周 (unit circle),
$S^{1}=\left\{x \times y \mid x^{2}+y^{2}=1\right\}$
其作为平面 $\mathbb{R}^{2}$ 的一个子空间. 设映射定义为 $f(t)=(\cos 2 \pi t, \sin 2 \pi t)$. 我们应用三角函数的性质推得 $f$ 是一个连续的一一映射. 但 是 $f^{-1}$ 不连续. 例如, 定义域中的开集 $U=\left[0, \frac{1}{4}\right)$ 在 $f$ 下的像不是 $S^{1}$ 中的开集, 这是由于不 存在 $\mathbb{R}^{2}$ 中包含 $p=f(0)$ 的开集 $V$, 使得 $V \cap S^{1} \subset f(U)$.
例1:$E^{n}$ 中的单位球体 $D^{n}:=\{x \in E^{n} | ||x|| \leqslant 1\}$ 的内部 $D^{\circ}$ 同胚于 $\boldsymbol{E}^{n} .$ 同胚映射 $f: (D^n)^{\circ} \rightarrow E^{n}$ 可规定为: $f(x)=\dfrac{x}{1-|x|}$, $\forall x \in (D^{n})^{\circ}$. 它的逆映射为:
例2:$\boldsymbol{E}^{n} \backslash\{O\} \cong \boldsymbol{E}^{n} \backslash D^{n}$ (O 为原点).
规定 $f: \boldsymbol{E}^{n} \backslash\{O\} \rightarrow \boldsymbol{E}^{n} \backslash D^{n}$ 为 $f(x)=x+\dfrac{x}{|x|}$. 其几何意义为每 一点背向原点 $O$ 移动单位长, 则 $f$ 是一一对应, 并且连续. $f^{-1}$ 是每一 点朝 $O$ 移动单位长, 也是连续的
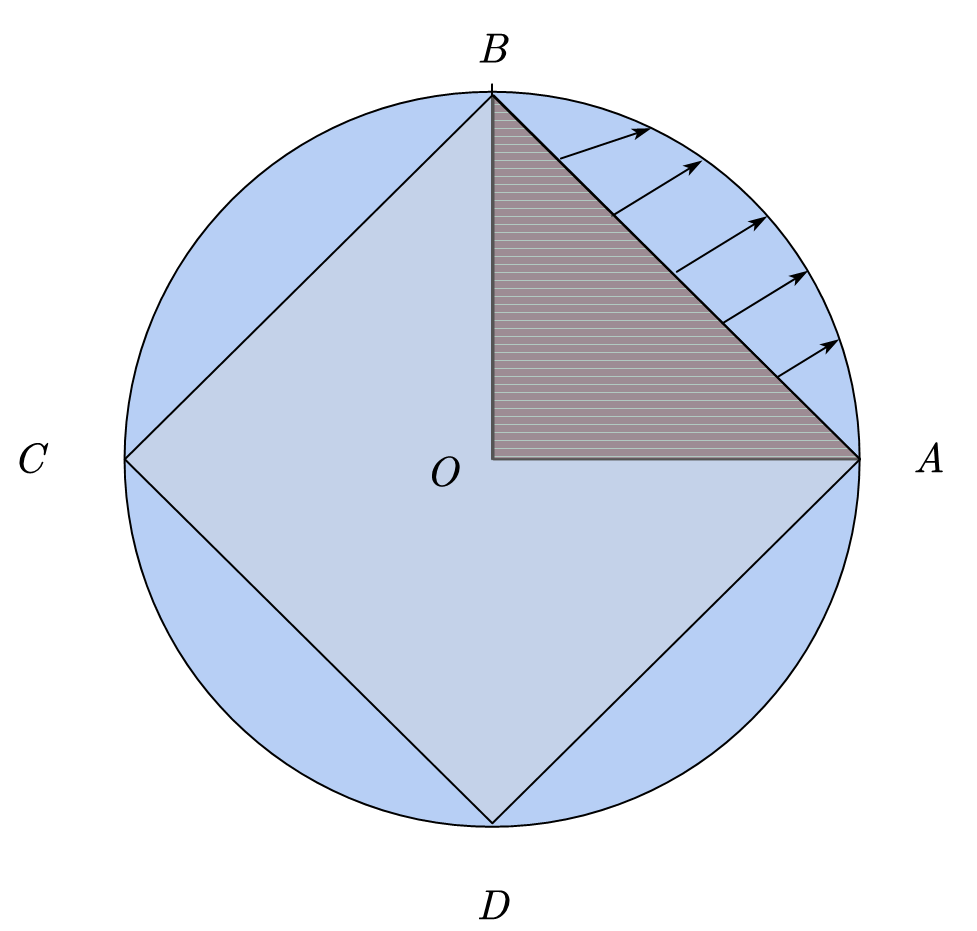
例3:任何凸多边形 (包含内部) 都互相同胚.
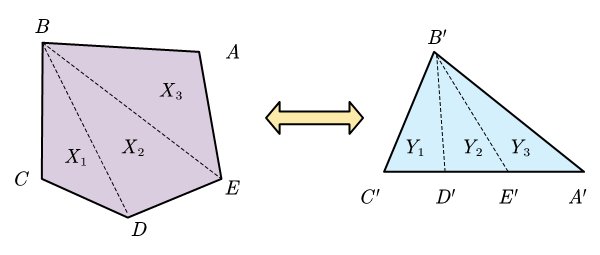
这里我们仅以凸多边形为五边形和三角形来说明这一这一问题,其他多边形证明方法是类似的!
如图中我们可以看到,五边形和三角型都被分割成了三份,在$X_i\to Y_i$上建立仿射变换$f_i$,又因为在边界上他们是相同的,因此课规定出$f:ABCDE\to A’B’C’$的一一映射,根据粘贴引理可知,他们同胚!
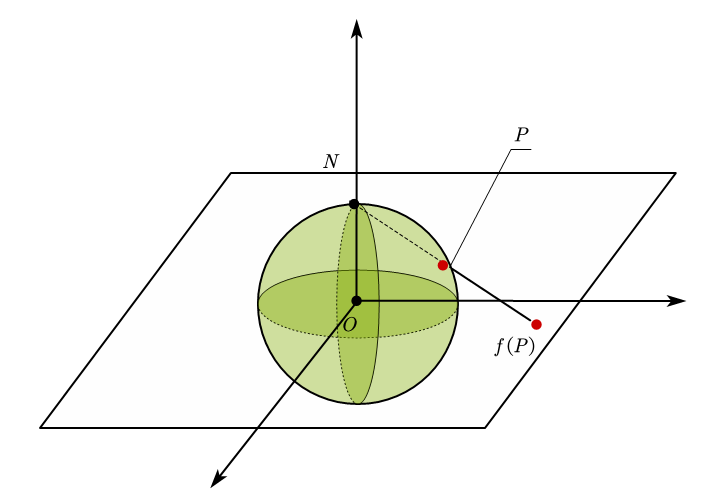
例4:球面 $S^{2}$ 去掉一点后与 $E^{2}$ 同胚. 球极投射就是把去掉北极 点的球面映射到赤道平面的一个同 胚映射它的分析表达
具体的几何表示如图所示.
例5:任何凸多边形和$D^2$同胚.
首先由于任何凸多边形都和一个边长为$\sqrt{2}$的正方形同胚的,因此我们只需要证明这个正方形同胚于单位圆盘即可!下边我们来叙述这件事情,定义映射:$f(x,y)=(\sqrt{x},\sqrt{y})$,这就是正方形到单位圆盘的一个映射,具体如图所示!
下边我们看一下,子空间中最重要的一个连续映射:投射.
投射
设 $\pi_{1}: X \times Y \rightarrow X$ 定义为$\pi_{2}: X \times Y \rightarrow Y$ 定义为
映射$\pi_{1}$ 和 $\pi_{2}$ 分别称为 $X \times Y$ 到它的第一因子和第二个因子上的投射 (projections).
不难验证$\pi_1$和$\pi_{2}$都是连续映射,比如对$\pi_{1}$而言,$X$中开集$U$的原像是$U\times Y$,而这显然就是$X\times Y$中的一个开集!且我们还有如下的定理!
定理:族$\mathcal{S}=\left\{\pi_{1}^{-1}(U) \mid U\right.$ 是 $X$ 中的开集 $\} \cup\left\{\pi_{2}^{-1}(V) \mid V\right.$ 是 $Y$ 中的开集 $\}$ 是 $X \times Y$ 的拓扑(我们之前定义的那种)的一个子基.
验证该定理并不是一件困难的事情!一般我们将这种方式生成的$X\times Y$的拓扑称为积拓扑,而将最开始我们定义的拓扑的方式称为箱拓扑,现在看来我们两者之间是没有差别的,但是我们为什么又非要区分呢?这是因为当我们想要将定义有限笛卡尔集上拓扑的方法推广到无穷笛卡尔集上定义拓扑的时候这两种拓扑是不同的!且两者在某些方面性态相差十分大!
无穷乘积空间
为了认识到两种拓扑的不同,我们需要将其放在无穷乘积拓扑空间中考察!为了定义无穷乘积空间上的拓扑,我们首先得先定义好无穷笛卡尔基!
定义:无穷笛卡尔积
设 $J$ 是一个指标集. 对于给定的集合 $X, X$ 的元素的 $J$-串 $(J$-tuple $)$ 定义为一个映 射 $\boldsymbol{x}: J \rightarrow X .$ 若 $\alpha$ 为 $J$ 的一个元素, 我们用 $x_{\alpha}$ 表示 $\boldsymbol{x}$ 在 $\alpha$ 处的值, 而再不用 $\boldsymbol{x}(\alpha)$ 表示这个值, 并且将它称为 $\boldsymbol{x}$ 的第 $\alpha$ 个坐标(coordinate). 我们将用记号
$\left(x_{\alpha}\right)_{\alpha \in J}$
表示函数 $x$ 本身. 这个“串记法”使我们将 $J$-串对于指标族的依赖表示得更明确些. 用 $X^{J}$ 表示 $X$ 中元素的 $J$-串的全体.
(最开始不方便理解时,我们仍然可以模仿 有限情况那样的理解,一个点有无穷个分量,每个分量分别是$x_{\alpha}$.)
定义: 设 $\left\{A_{\alpha}\right\}_{\alpha \in J}$ 是一个加标集族, $X=\bigcup_{\alpha \in J} A_{\alpha}$. 加标集族 $\left\{A_{\alpha}\right\}_{\alpha \in J}$ 的笛卡儿积 (Cartesian product), 定义为使得对于每一个 $\alpha \in J$ 有 $x_{\alpha} \in A_{\alpha}$ 的 $X$ 的元素的所有 $J$-串 $\left(x_{\alpha}\right)_{\alpha \in J}$ 的集合, 用 $\prod A_{\alpha \in J}$
表示. 也就是说, 它是所有这样的函数的集合, 这些函数要求满足条件: 对于每一个 $\alpha \in J$ 有 $x(\alpha) \in A_{\alpha}$.
当指标集无需强调时,有时我们也用 $\Pi A_{a}$ 表示上述笛卡儿积, 其元素则记为 $\left(x_{a}\right)$. 当所有的 $A_{a}$ 都等于同一个集合 $X$ 时, 笛卡儿积 $\prod_{\alpha \in J} A_{\alpha}$ 恰为所有 $X$ 的元素的 $J$-串的集合 $X^{J}$.
对于 $X^{J}$ 的元素, 我们有时使用“串记法”表示,有时使用函数表示, 依方便而定.
箱拓扑
设 $\left\{X_{\alpha}\right\}_{\alpha \in J}$ 是拓扑空间的一个加标族. 积空间上的某一个拓扑的基取为所有形如上的某一个拓扑的基取为所有形如
的集合的族, 其中对于每一个 $\alpha \in J, U_{a}$ 在 $X_{a}$ 中是开的. 由这个基生成的拓扑叫做箱拓扑 (box topology).
这种拓扑的定义其实是我们最开始拓扑基定义的推广!回忆一下那时我们拓扑基是这样的:
$\mathscr{B}=$若干个$ U\times V $的并,$U,V $是$X,Y$中的开集
这里只不过是将有限个换为无穷个而已!
另一种则是用子基定义的:设函数
将笛卡儿积空间的每一个元素对应其第 $\beta$ 个坐标, 即
我们把 $\pi_{\beta}$ 称为关于指标 $\beta$ 的投射 (projection mapping).
[积拓扑]
今 $S_{\beta}$ 表示族今 $S$ 为所有族 $S_{\beta}$ 的并
子基 $S$ 生成的拓扑称为积拓扑 (product topology). 给定了这个拓扑的 $\prod_{a \in J} X_{a}$ 称为积空间 (product space).
现在我们比较一下积拓扑和箱拓扑的基元素的不同点是什么:
对于箱拓扑而言,每个$U_{\alpha}$是$X_{\alpha}$中的开集,而对于积拓扑,只有有限个$U_{\alpha}$是$X_{\alpha}$中的开集,而剩下的$U_{\alpha}$都是$X_{\alpha}$中的全集.这帮我们看清楚了两种拓扑中元素的的不同,但是哪个更拓扑更良好一些呢?事实上我们更偏爱积拓扑,我们后边会举出多个例子来说明这一原因.
下边的几个事实我们仅作罗列不加证明:
- 设对于每一个 $\alpha \in J, A_{\alpha}$ 是 $X_{\alpha}$ 的一个子空间, 则当两者都用箱拓扑或者两者都 用积拓扑时, $\Pi A_{\alpha}$ 是 $\Pi X_{a}$ 的一个子空间.
- 若每一个空间 $X_{a}$ 都是 Hausdorff 的, 则无论是箱拓扑还是积拓扑, $\Pi X_{a}$ 都是 Hausdorff 的.
- 设 $\left\{X_{a}\right\}$ 是一个加标空间族, 对每一个 $\alpha$ 有 $A_{a} \subset X_{a}$. 若对 $\Pi X_{\alpha}$ 赋予积拓扑或者 赋予箱拓扑, 则有
接下来的一个定理会告诉我们为什么我们更偏爱积拓扑:
定理映射 $f: A \rightarrow \prod_{\alpha \in J} X_{\alpha}$ 定义为
其中对每一个 $\alpha, f_{a}: A \rightarrow X_{a}$. 设 $\Pi X_{a}$ 具有积拓扑, 则 $f$ 连续当且仅当每一个函数 $f_{\alpha}$ 连续.
证明:一个方向是显然的:如果$f$是连续的,那么$f_{\alpha}$也是连续的.
设$\pi_{\beta}$是$\Pi X_{\beta}\to X_{\beta}$的投射,那么$f_{\alpha}=\pi_{\beta}\circ f$,连续函数的复合是连续映射,因此$f_{\alpha}$是连续映射;
反之我们只需要在证明任何一个子基的原像是开集即可.积拓扑的一个子基元素是:$\pi_{\beta}^{-1}\left(U_{\beta}\right)$,其中$U_{\beta}$是$X_{\beta}$中的开集.我们求$\pi_{\beta}^{-1}\left(U_{\beta}\right)$原像是开集即可.而因为:$f_{\alpha}=\pi_{\beta}\circ f$,所以:
因此子基的原像是开集,连续性得证.
但是箱拓扑就没有这样的性质了,给出直接的反面证明是不现实的,我们给出反例来说明:
反例
考虑 $\mathbb{R}$ 的可数无限积 $R^{\omega}$.对于每一个 $n \in \mathbb{Z}_{+}, X_{n}=\mathbb{R}$. 函数 $f: \mathbb{R} \rightarrow \mathbb{R}^{\omega}$ 定义为
其第 $n$ 个坐标函数是 $f_{n}(t)=t$. 每一个坐标函数 $f_{n}: \mathbb{R} \rightarrow \mathbb{R}$ 都连续, 所以当赋予 $\mathbb{R}^{\omega}$ 积拓扑时, $f$ 是连续的. 而当 $\mathbb{R}^{\omega}$ 给的是箱拓扑时, $f$ 不连续. 例如, 取箱拓扑的基元素
我们断言: $f^{-1}(B)$ 不是 $R$ 中开集. 事实上, 如果 $f^{-1}(B)$ 是 $R$ 中开集, 它必定包含 0 旁边的某 一个区间 $(-\delta, \delta)$, 也就是说 $f((-\delta, \delta)) \subset B$. 将 $\pi_{n}$ 作用于这个包含关系的两边, 可见对于 所有 $n$,
这是一个矛盾.
箱拓扑糟糕的性质远非这些,我们在度量拓扑中会再次介绍.
度量拓扑-2
我们之前已经介绍过了度量拓扑,基本内容请在前边中回顾.
下边我们不加证明的给出一些度量空间中的性质;这些性质读者大部分在泛函分析或者数学分析中已经学过了,如果没学过可以查阅任何一本泛函分析的书籍!
- 设 $f: X \rightarrow Y, X$ 和 $Y$ 是分别具有度量 $d_{X}$ 和 $d_{Y}$ 的可度量化空间. 那么 $f$ 的连 续性等价于:对给定的 $x \in X$ 和 $\varepsilon>0$, 存在 $\delta > 0$, 使得
- (序列引理(sequence lemma))设 $X$ 是一个拓扑空间, $A \subset X$. 若 $A$ 中有一个收敛于 $x$ 的序列, 则 $x \in \bar{A}$. 若 $X$ 为可度量化空间, 则逆命题也成立.
- 设 $f: X \rightarrow Y$. 若 $X$ 为可度量化的空间, 则 $f$ 连续的充分必要条件是对于 $X$ 中 每一个收敛序列 $x_{n} \rightarrow x$, 序列 $f\left(x_{n}\right)$ 收敛于 $f(x)$.(我们之前已经说过了,该定理对一般的拓扑空间是不正确的.)
- (一致极限定理 (uniform limit theorem) )设 $f_{n}: X \rightarrow Y$ 是从拓扑空间 $X$ 到度量 空间 $Y$ 的连续函数的一个序列. 若 $\left(f_{n}\right)$ 一致收敛于 $f$, 则 $f$ 连续.
注意到:当一个空间给定时,尤其是这个空间是较好的空间,比如度量空间、赋范空间、内积空间,我们证明时可以完全使用这个空间的手法,而不必非要用拓扑的语言说话(那是十分繁琐的.)但是当一个拓扑空间只是一般的空间,那么此时我们叙述时就需要用拓扑的语言说话了,这是值得注意的!
现在回到我们的正题,我们为何要再回头来研究度量空间?主要是想要再次讨论一个拓扑空间是否可以度量化?最重要的一个就是我们能否在一般的乘积空间引入度量?能够将无穷乘积空间的嵌入度量空间中?现在我们以$\mathbb{R}^{\omega}$为例,我们知道在$\mathbb{R}^n$上有度量,比如二范数:$\displaystyle [\sum_{k=1}^{n}(x_i-y_i)^2]^{\frac{1}{2}}$.那我们能否自然的将$\mathbb{R}^{\omega}$上的范数定义为:
答案是否定的!因为这面临着上述无穷求和是否收敛的问题,显然对于一般的$x,y$而言上述无穷求和不收敛!一个想法是:我们对每个坐标赋予权重:比如第$i$个权重为$\frac{1}{n}$很遗憾的是:这一操作不可行,比如你就取每个坐标为$(1,2,\cdots,n,…)$和$(0,0,\cdots,0…)$显然这个无穷级数还是不能收敛!那这不失为一个好方法!当无穷乘积的每个分量只是$[0,1]$而非$\mathbb{R}$时,这一操作是可行的!但是我们想要建立一个一般性的度量,那怎么办呢?下边提供了一种方法:
[标准有界度量]:设 $X$ 是具有度量 $d$ 的一个度量空间. 则用
所定义的 $\bar{d}: X \times X \rightarrow \mathbb{R}$ 是一个度量, 并且 $\bar{d}$ 和 $d$ 诱导出的拓扑是 $X$ 的同一个拓扑.
度量 $\bar{d}$ 称为相应于 $d$ 的标准有界度量 $A$ (standard bounded metric).
证明这是一个度量不难,只需要分类讨论即可!又因为以$B(x,\frac{1}{2})$全体可以作为$X$上的拓扑基,而$d$和$\bar{d}$的$\frac{1}{2}$邻域球是相同的,因此他们有相同的拓扑基,因此他们是相同的拓扑!
[一致拓扑]:
给定指标集 $J$ 以及 $R^{J}$ 中的点 $\boldsymbol{x}=\left(x_{\alpha}\right)_{\alpha \in J}$ 和 $\boldsymbol{y}=\left(y_{\alpha}\right)_{\alpha \in J}$, 定义 $\mathbb{R}^{J}$ 的一个度量 $\bar{\rho}$ 为
不难证明这是一个度量!
下边我们来看看在$\mathbb{R}^{J}$上他和箱拓扑以及积拓扑的关系:
[定理]$\mathbb{R}^{J}$ 上的一致拓扑细于积拓扑, 粗于箱拓扑. 当 $J$ 为无限集时, 这三个拓扑两 两不同.
由于当$J$是有限集时,积拓扑和箱拓扑是一个拓扑,因此如果结论成立时,自然三者是相同的;现在我们证明一致拓扑细于积拓扑而粗于箱拓扑!然后说明当$J$为无穷时,三者不相同!想要比较拓扑的粗细一种方法是直接看拓扑之间有没有包含关系;一种就是比较两者的拓扑基。对于一般的拓扑而言往往前者是不容易看出来的,因此常用后者,而我们之前已经介绍了一个很有用的定理了!参见定理.
下边我们用前面引用的定理来证明该定理:
一致拓扑细于积拓扑:取积拓扑中一个包含$x$的一个基元素:它具有以下形式:
其中仅有有限个位置$U_{\alpha}$是包含的$x_{\alpha}$的开球(为对应$X_{\alpha}$中的拓扑基中的元素),剩余的$U_{\alpha}$都是$R$.我们不妨记这个基元素为:
令$\varepsilon=\min \{r_1,\cdots r,_n\}$,则$B(x,\varepsilon)\subset \Pi U_{\alpha}$中.
箱拓扑细于一致拓扑:考察一致拓扑下包含$x$的一个开球:$B(x,r)$,那么我们取:
则显然他在开球中.
下边证明无穷情况下三者两两不同.
取箱拓扑中元素:
则一致拓扑中包含0的开球中都不在该基元素中,故箱拓扑严格细于一致拓扑.
同理取一致拓扑中基元素:
则积拓扑中也没有元素包含在这个开集中.
现在我们已经可以在无穷乘积空间中定义度量了,那么问题来了,存不存在一种度量使其和箱拓扑或者积拓扑一致呢?接下来我们将证明在可数情况下,积拓扑可度量化,而其他无穷情况下都不可行!
[嵌入定理]: 设 $\bar{d}(a, b)=\min \{|a-b|, 1\}$ 是 $\mathbb{R}$ 上的标准有界度量. 对于 $\mathbb{R}^{\omega}$ 的两个点 $\boldsymbol{x}$, $y$, 定义
那么 $D$ 是诱导 $R^{\omega}$ 的积拓扑的一个度量.
我们先分两个步骤:第一:证明这是个度量!第二:再分两个小步骤:两种拓扑互相包含!最终得到结论:$\mathbb{R}^{J}$可以嵌入某个度量空间中!
所有的 $i$ 有
因而
现在我们又要用定说明两种拓扑相同了!
首先:我们任取度量拓扑中一个开集:$x\in U$,那么必然存在一个开球$B(x,r)$在$U$中,取$N$充分大,使$\frac{1}{N} < r$.那么:考虑:
我们来证明 $V \subset B_{D}(\boldsymbol{x}, \varepsilon):$ 对于 $\mathbb{R}^{\omega}$ 中的任意一点 $\boldsymbol{y}$ 以及 $i \geqslant N$,
因此
如果 $\boldsymbol{y}$ 在 $V$ 中, 上面的式子小于 $\varepsilon$, 于是 $V \subset B_{D}(\boldsymbol{x}, \varepsilon)$, 这便是所要证的.
反之,考虑积拓扑中的一个元素:
其中在$i=1,2,\cdots,n,U_i\ne R$其他位置均为$R$.可以记该元素为:
我们取
事实上, 设 $\boldsymbol{y}$ 是 $B_{D}(\boldsymbol{x}, \boldsymbol{\varepsilon})$ 的一个点, 那么对于所有的 $i$,
因此 $\bar{d}\left(x_{i}, y_{i}\right)<\varepsilon_{i} \leqslant 1$. 由此推出 $\left|x_{i}-y_{i}\right|<\varepsilon_{i}$. 因此, $\boldsymbol{y} \in \Pi U_{i}$.故命题得证!我们得到了$\mathbb{R}^{\omega}$可以被度量化!
那其他情况下呢?我们刚刚已经说了:其他无穷情况和箱拓扑情均不可度量化!证明他们的方法竟然是利用度量空间的性质!
反例
$\mathbb{R}^{\omega}$ 在箱拓扑下是不可度量化的
我们将证明序列引理对 $R^{\omega}$ 不成立. 设 $A$ 为 $R^{\omega}$ 中所有坐标都是正数的点所组成的那个子 集, 即
设 0 是 $R^{\omega}$ 的 “原点”, 即零点 $(0,0, \cdots)$, 它的每一个坐标都是 0 . 在箱拓扑中, $0 \in \bar{A}$, 这是因 为, 如果
是含有 0 的任意一个基元素, 则 $B$ 与 $A$ 相交, 比如点
就属于 $B \cap A$.
但是, 我们可以断定在 $A$ 中没有收敛于 0 的点的序列. 对于 $A$ 中的序列 $\left(a_{n}\right)$,
其中每一个坐标 $x_{\text {in }}>0$, 这就可以构造出 $R$ 的箱拓扑的基元素 $B^{\prime}$,
$B^{\prime}$ 含有原点 $\mathbf{0}$, 却不包含序列 $\left(\boldsymbol{a}_{n}\right)$ 的元素: 这是因为 $\boldsymbol{a}_{n}$ 的第 $n$ 个坐标 $x_{m}$ 不属于区间 $\left(-x_{n n}, x_{n n}\right)$. 所以点 $a_{n}$ 不可能属于 $B^{\prime}$. 因此在箱拓扑下, 序列 $a_{n}$ 不收敛于 0 .
这里证明的方法依赖于度量空间良好的性质!其实是可数性和分离性的体现!
定理:不可数个 $R$ 的积空间是不可度量化的.
设 $J$ 为不可数指标集. 我们来证明: $R^{J}$ 在积拓扑下不满足序列引理.
设 $A$ 为 $R^{J}$ 的子集, 其元素 $\left(x_{a}\right)$ 满足:除了有限个 $\alpha$ 之外, 对其余所有的 $\alpha$ 有 $x_{\alpha}=1$. 令 0 为 $\mathbb{R}^{J}$ 的 “原点”, 它的所有坐标都是 0 .
可以论断 0 属于 $A$ 的闭包. 事实上, 令 $\Pi U_{a}$ 为含有 0 的一个基元素, 那么仅对有限个 $\alpha$,比如 说 $\alpha=\alpha_{1}, \cdots, \alpha_{n}$, 有 $U_{\alpha} \neq \mathbb{R}$. 设 $\left(x_{\alpha}\right)$ 为 $A$ 中一点, 对于 $\alpha=\alpha_{1}, \cdots, \alpha_{n}$, 取 $x_{\alpha}=0$. 对其余所有的 $\alpha$, 取 $x_{\alpha}=1$. 那么 $\left(x_{\alpha}\right) \in A \cap \Pi U_{\alpha}$, 这便证明了 $0 \in \bar{A}$.
但是 $A$ 中不存在收敛于 0 的点的序列. 我们对此证明如下: 设 $\left(a_{n}\right)$ 为 $A$ 的点的一个序列. 给定 $n$, 设 $J_{n}$ 表示指标集 $J$ 的子集, 其元素 $\alpha \in J_{n}$ 是使 $\boldsymbol{a}_{n}$ 的第 $\alpha$ 个坐标异于 1 的指标. 集合 $J_{n}$ 的并是有限集的可数并, 因而是可数的. 但是 $J$ 不可数, 那么 $J$ 中必有一个指标, 比如说 $\beta$, 使得它不在每一个 $J_{n}$ 中. 这就是说: 对于每一个点 $a_{n}$, 都有它的第 $\beta$ 个坐标等于 1 .
令 $U_{\beta}$ 为 $R$ 中的开区间 $(-1,1), U$ 为 $R^{J}$ 的一个开集 $\pi_{\beta}^{-1}\left(U_{\beta}\right)$. 那么 $U$ 是 0 的一个邻域, 并且它不包含任何点 $\boldsymbol{a}_{n}$. 所以序列 $\left(\boldsymbol{a}_{n}\right)$ 不可能收敛于 $\mathbf{0}$.
不是很容易理解,可以暂时记住结论,回头看!